Quantum information cannot be copied
Suppose the No-Cloning principle did not exist, and you would have been able to clone an unknown quantum state. The quantum state is in an unknown superposition of the 0 and 1 state. How would you find out the weights of the superposition, i.e. the respective probabilities of finding the state in 0 or 1?
If we could clone the qubit, we could make many copies of the unknown quantum state. Then we can measure each qubit and make a histogram of the measurement outcomes (0 or 1). If we have enough copies, the number of times we have measured an outcome is a good estimate for the probability that the state was in the 0 or 1 state.
Example: suppose this is the outcome of such a repeated measurement experiment:
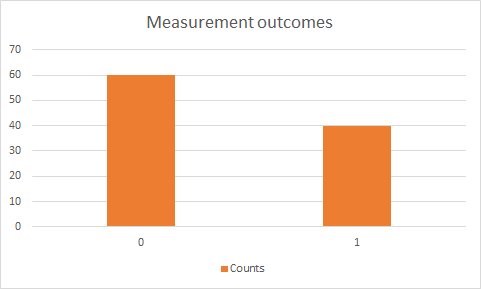
We counted 60 zero's and 40 ones. Then we know that the state superposition was roughly for 60% in the 0 state and for 40% in the 1 state.